Partire da un segno per sviluppare un progetto in 3D può essere un buon approccio, se questo segno si ripete in varie dimensioni e spazialità può costituire un elemento caratterizzante efficace. La serie dello stesso segno restituisce poi un effetto visivo piacevole che può essere esperito anche con altri sensi. Il genio di Escher è stato preso come spunto da Francesco Cantini, allievo di Design della LABA, per progettare lo spazio e gli oggetti specifici.
“Il fenomeno dello strano anello racchiude in se il concetto di infinito: l’infinito potenzialmente negativo, che non finisce mai e l’infinito attuale, perfetto e chiuso. Il primo detto anche falso infinito, è caratterizzato dalla ripetizione all’infinito di una medesima operazione di divisione (concezione efficacemente rappresentata da Sisifo, condannato a trasportare in eterno sulla sommità di un monte un masso che, appena giunto in cima rotolava a valle). Il secondo, l’infinito attuale, è un infinito chiuso e, per così dire, compiuto, identificabile cosmologicamente con l’ universo. I greci non lo nominavano mai in matematica e cercavano il più possibile di evitarlo in quanto creava problemi difficilmente risolvibili.”
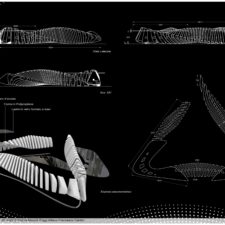
La galleria è pensata per essere collocata nelle campagne di Leeu-warden, in Olanda, città natale di Escher. Dalla pianta dell’edificio si evince l’importanza del percorso museale strutturato sul concetto dell’eterno ritorno e dell’infinito. Il percorso può essere completato senza mai tornare indietro.
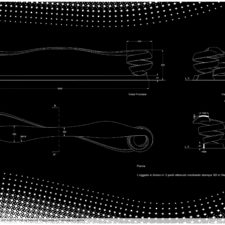
Mob é un bancone costruito sul principio del nastro di Mobius. Si passa idealmente da da una faccia all’altra senza staccare lo sguardo dall’oggetto. Un’esperienza sensoriale continua.
In matematica, il nastro di Mobius è un esempio di superficie non orientabile e di superficie rigata. Le superfici ordinarie, ossia le superfici che nella vita quotidiana siamo abituati ad osservare, hanno sempre due facce, per cui è sempre possibile percorrerne idealmente una senza mai raggiungere l’altra, se non attraversando una linea di demarcazione costituita da uno spigolo (chiamato “bordo”): si pensi ad esempio al cilindro. Per queste superfici è possibile stabilire convenzionalmente un lato “superiore” o “inferiore”, oppure “interno” o “esterno”. Nel caso del nastro di Mobius, invece, tale principio viene a mancare: esiste un solo lato e un solo bordo. Dopo aver percorso un giro, ci si trova dalla parte opposta. Solo dopo averne percorsi due ci ritroviamo sul lato iniziale.
Si potrebbe passare da una superficie a quella “dietro” senza attraversare il nastro e senza saltare il bordo ma semplicemente camminando all’infinito. Un nastro di Mobius può essere realizzato partendo da un parallelepipedo a base triangolare ed unendone i lati corti dopo aver impresso ad uno di essi mezzo giro di torsione (180°). A questo punto se si percorre il nastro con una matita, partendo da un punto casuale, si noterà che la traccia si snoda sull’intera superficie del nastro, che è quindi unica. Essendo una superficie rigata, per ogni punto sul nastro passa almeno una retta che giace sulla superficie del nastro.”
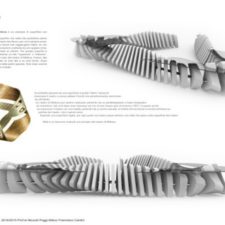
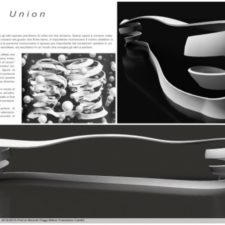
Il Nastro infinito Bond of Union è un elemento decorativo che ha come unico scopo quello di far riflettere sulla continuità di pensiero. L’oggetto di arredo destruttura la volontà di prevalere sulle idee altrui per dare più valore alla generazione congiunta di idee.
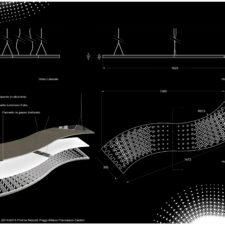
Fractal è una lampada a sospensione ispirata a Escher. La divisione regolare del piano è l’insieme di forme chiuse che ricoprono il piano completamente senza sovrapporsi.